MATLAB学习

先来软件的操作界面

首先分为几个区域：

• 当前文件夹：显示当前的文件目录，及根目录下的文件和目录。
• 编辑器：初始时没有这个界面，用于编辑matlab文件（.m文件），如果没有打开任何脚本文件就不会出现这个界面。有点击一个脚本才会显示。
• 命令行窗口：用来执行一些快捷的指令，可看成脚本的指令化。
• 工作区：主要显示变量和对应值（基本运算后会自动生成ans变量）。

清除历史和注释

清除的两种方式：

• 用clc命令可清除命令行窗口的历史记录
• 用clear all指令可以清空工作区中的所有变量（但没有clc的功能）

注释一般出现在脚本中：

​ 用%之后可写注释行

​ 用%%可隔开代码段

clear all  % 清除workspace中的所有变量
clc  %清除Command Window中所有命令

变量类型

数字，字符串，矩阵

class()函数可以查询到变量的类型，类似于python中的type()

数字和字符串

和python类似，还是直接赋值，eg：

age = 12
gender = 'male'
abs('s')		% abs()是指绝对值函数没问题，但是它同时还可以转化字符为ascii码
char(97)		% 转化数字为对应ascii码的字符
num2str(65)		% 转化数字为字符串

describ = 'I Love MATLAB'
length(describ)		% 计算字符串的字符个数

矩阵

矩阵在matlab中的赋值非常的简单，类似于python中的列表和元组的复合

基本矩阵建立：

>> A = [1, 2, 3; 4, 5, 6; 7, 8, 9]

A =

     1     2     3
     4     5     6
     7     8     9

很容易看出矩阵的每个元素是用,来分隔的（你可以只用,或空格），每一行是用;分隔的。

矩阵的变换和运算

B = A'		% B变成A的转置矩阵
C = A(:)	% 将矩阵A拉伸为一列（按列拉）
D = inv(A)	% 求逆矩阵（注意需要是方阵）
E = eye(3)	% 生成一个3*3的单位矩阵
F = magic(5)	% 生成一个5阶幻方

%%
E = zeros(10, 5, 3)		% 创建一个共3个维度的10行5列的零矩阵
% 每个维度可以这样表示或得到
E(:, :, 1)		% 这是一维，以此类推
E(:, :, 2)
E(:, :, 3)

重要函数

生成随机数

rand()生成均匀分布的伪随机数，分布在（0 ~ 1）之间，eg：

rand(10, 5)		% 生成10行5列的均匀分布的伪随机数矩阵
rand(10, 5, 'double')	% 'double'这里是指令的精度类型（双精度），可选值还有'single'
rand(RandStream, 10, 5)	% RandStream是随机种子

randn()生成标准正态分布的伪随机数（均值μ为0， 方差σ为1），用法和rand()类似

randi()生成的是伪随机整数，eg：

randi(iMax, m, n)	% 在区间(0, iMax)生成随机矩阵
randi([iMin, iMax], m, n) 	% 在区间(iMin, iMax)生成随机矩阵

ps：这三个函数都可以单独使用，调用后生成一个随机数。

特殊类型

元胞数组

元胞数组是matlab中特有的一种数据类型，是数组的一种。内部可以是属于不同数据类型的数据，有点类似于C的结构体或者python的字典。
它的特性给人一种查询数据的感觉，可以一直追踪到所有变量都被翻译成基本的数据信息。其class()返回值为cell。

建立类型：

A = cell(1, 6)		% 建立一个1行6列的元胞数组
A{2}		% 获取到元胞数组中的第二个元素，和其他语言数组不一样(用[])

结构体

matlab的结构体并不是C中的结构体，而更像是python中的字典类型

举个栗子：

books = struct('name', {{'Vue Framework', 'Big Data'}}, 'price', [30, 40])
% 就是一个键值对
books.name		% 这就得到了books的name属性
books.name(1)	% 这里取出name的第一个
books.name{1}	% 注意()取出的是cell，{}取出的才是值

你会注意到这里的键值对全是用,隔开的，而且字符串用{}，数字用[]

矩阵扩展

先前已经说过矩阵可以用[]来构造，然后还有其他构造方法：

>> A = [1:2:9]A =     1     3     5     7     9

这样我们生成一个一行矩阵，这一行中范围是1 ~ 9，步长是2。

>> B = repmat(A, 3, 1)B =     1     3     5     7     9     1     3     5     7     9     1     3     5     7     9     >> C = repmat(A, 3, 2)C =     1     3     5     7     9     1     3     5     7     9     1     3     5     7     9     1     3     5     7     9     1     3     5     7     9     1     3     5     7     9

repmat()函数显而易见是一个重复构造的函数，重复构造m行n列

>> D = ones(4, 4)D =     1     1     1     1     1     1     1     1     1     1     1     1     1     1     1     1

ones()即生成m行n列的全一矩阵

矩阵四则运算

A = [1 2 3 4; 5 6 7 8]B = [1 1 2 2; 2 2 1 1]C = A + B 	% 矩阵的加法D = A - B 	% 矩阵的减法E = A * B'	% 乘法，注意这里需要转置F = A .* B 	% 对应项相乘，不是矩阵乘法(.都是代表对应项)G = A / B 	% 这相当于A * inv(B)H = A ./B 	% 对应项相除

矩阵下标

A = magic(5)B = A(2, 3)		% 取到2行3列的元素C = A (3, :)	% 取出第3行所有元素(即取出第三行)[m, n] = find(A > 20)	% 这里是找到的元素的索引值放到m和n中

循环和分支结构

循环

直接看例子：

%% 求1到5的平方和sum = 0;for n = 1:5sum = sum + n ^ 2;endsum

这里n = 1:5是从1循环到5，中间默认步长为1（也就是说还可以写一个1:1:5）不管是哪种结构，都是要写end的。注意在脚本中一个语句还是要写;

再来一个嵌套结构：

%% 实现1到5的阶乘和sum = 0;for i = 1:5	p = 1;		for j = 1:i			p = p * j;		end	sum = sum + p;endsum

注意这里嵌套之后出现了类似python的缩进结构，这是matlab在嵌套结构中必须具备的（否则出错），但是建议没有嵌套时还是保持缩进结构（良好的规范）

while

%% 1到10的求和s = 0;n = 1;while n <= 10	s = s + n;	n = n + 1;end

分支

老规矩，直接上代码：

if a > b	'成立语句';elseif a < b	'成立语句';else	'不成立语句';endswitch 表达式(数值或字符串)	case 数值或字符串		语句1;	case 数值或字符串		语句2;	otherwise		语句n;end

二维平面绘图

对于matlab的绘图，既然matlab是科学计算软件，则肯定是根据函数来画图。于是就要先有函数：f(x)

x = 0: 0.01: 2 * pi		% 很明显这里的x是离散型的y = sin(x)		% 建立了函数figure			% 建立一个幕布（就理解成canvas算了）plot(x, y)		% 绘制图形，类似python中的matplotlib用法title('y = sin(x)')		% 给图加个标题xlabel('x')		% 指定x轴标示ylabel('sin(x)')	% 指定y轴标示xlim([0 2*pi])		% 限定x定义域范围为(0, 2Π)

颜色选项表

颜色	字符
红	r
绿	g
蓝	b
黄	y
粉红	m
青	c
白	w
黑	k

线型选项表

线型	符号
实线	-
虚线	—
冒号线	:
点画线	-.

绘图高级

x = 0: 0.01: 20;y1 = 200 * exp(-0.05 * x) .* sin(x);y2 = 0.8 * exp(-0.5 * x) .* sin(10 * x);figure[AX, H1, H2] = plotyy(x, y1, x, y2, 'plot');% 这里的plogyy是表示两个函数y1,y2共用一个坐标系，然后画出图形% 画图的类型为'plot'set(get(AX(1), 'Ylabel'), 'String', 'Slow Decay')set(get(AX(2), 'Ylabel'), 'String', 'Fast Decay')% 这两句是设置每个函数的因变量名xlabel('Time (\musec)')title('Multiple Decay Rates')% 下面两句就是对两个函数线型的设置set(H1, 'LineStyle', '--')set(H2, 'LineStyle', ':')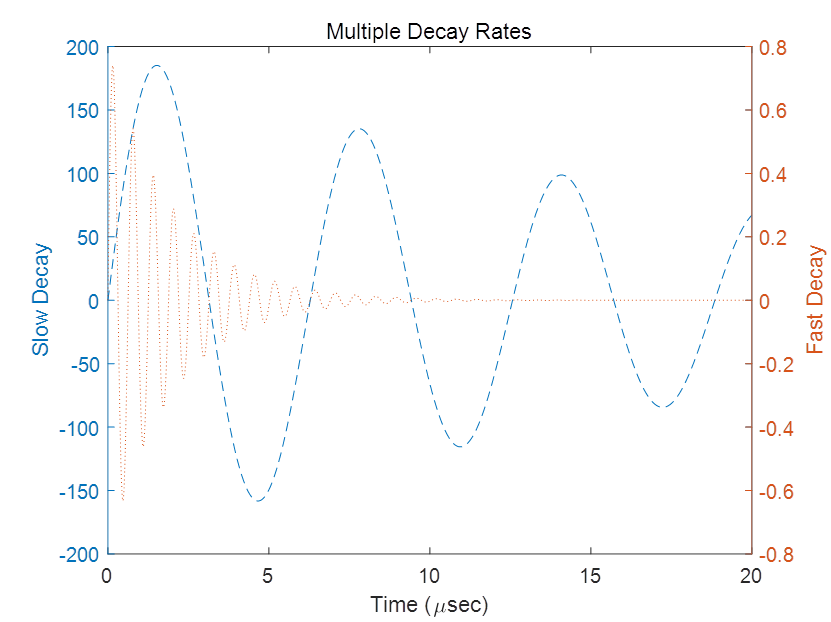

使用figure打开画布，使用close关闭画布

多图绘制

使用subplot()来绘制，参数解释：

• 第一个参数定义行数
• 第二个定义列数
• 第三个表示这张图对应的位置

比如subplot(2,2,1)就是两行两列共四个区域的第一个位置，subplot(2,1,2)就是两行一列两块区域的第二个位置（需要在每次定义subplot()之后重新定义图形）

三维立体绘图

t = 0: pi/50: 10*pi;% 记住二维绘图是plot，三维就是plot3plot3(sin(t), cos(t), t)xlabel('sin(t)')ylabel('cos(t)')zlabel('t')grid on		% 在图像中加入网格线axis square		% 将网格变成正方形

如果要暂时保存图形，继续绘制就用hold on

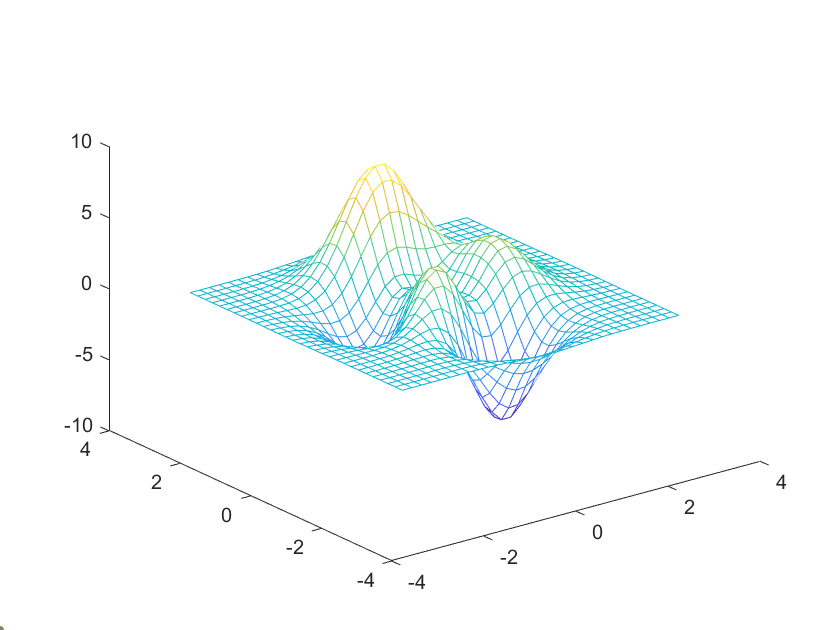
hold on...		% 其他图形代码hold off 	% 关闭图形的hold on状态

稍微引入双峰函数

[x, y, z] = peaks(30);
mesh(x, y, z)
grid

可以给论文平添一点高大上。

函数求解

首先是数据拟合，这里有很多好用的函数

• y = polyval(p, x)：求多项式p在x处的值y，x可以是一个点或者多个点。
• p3 = conv(p1, p2)：返回这两个多项式的乘积
• [p2,r] = deconv(p1, p2)：p3返回多项式p1除以p2的商，r返回余项
• x = roots(p)：用来求p的根
• p = polyfit(x, y, k)：用k次多项式拟合向量数据(x, y)，返回多项式的降幂系数

进行函数拟合的步骤（多项式函数拟合）：

1. 求出函数参数p，使用p = polyfit()
2. 求出拟合后的yfit值，使用yfit = polyval()
3. 对两者进行画图比较

使用最小二乘法进行拟合

[c, Q] = lsqcurvefit(Fun, c0, x, y, lb, ub)

求极值

x = fzero(Fun, x0)：返回一元函数Fun的一个零点

[x, f, h] = fsolve(Fun, x0)：

• x返回多元函数Fun，在x0附近的一个零点
• f返回Fun在x的函数值
• h如果大于零，结果可靠